Tartalomjegyzék
Műveletek mátrixokkal
- Szerző: Sallai András
- Copyright © 2014, Sallai András
- Licenc: CC BY-SA 4.0
- Web: https://szit.hu
A mátrixokról
A mátrixok tulajdonképpen számok téglalap alakú tömbjei. A mátrixokkal való műveletvégzés a tudományos számítások alapjai.
Fogalmak
Meghatározás
Számok táblázatos formában, amelynek n darab sora és m darab oszlopa van.
Példák
3×4 mátrix:
Szögletes zárójelek helyett lehet szimpla zárójel is.
Mátrix indexekkel
A mátrixban minden elemre tudunk hivatkozni az indexük alapján. Az első index a sor jelöli, a második az oszlopot.
A azt jelenti, az első sor, harmadik eleme.
Ha általánosan valamelyik elemre hivatkozunk akkor szokásos forma: .
Ahol i sor, j az oszlop.
Főátló
A főátlót azok az elem alkotják, amelyek sor- és oszlopindexei azonosak.
A fenti mátrixban főátlót a 8 5 és 3-as értékek alkotják, amelyeknek az indexe rendre: 11, 22, 33.
Determináns
A determinánsról
Minden mátrixhoz hozzárendelhető egy szám, amelyet determinánsnak nevezünk.
Ha a determináns 0, akkor szinguláris mátrixról beszélünk.
Ha determináns nem 0, akkor reguláris mátrixról beszélünk.
2x2-s mátrix
A determinánst számítása 2×2 mátrixban:
- veszem a fő átló elemeinek szorzatát
- veszem a másik átló elemeinek szorzatát
- a két szorzat különbsége a determináns
A determináns jelölése:
|A|
vagy:
det(A)
Legyen egy 2×2-es mátrix:
Kifejtési tétel
Ha kvadratikus mátrix mérete nagyobb mint 2, a determináns számítása másként történik.
A kifejtéshez ki kell választani egy sort vagy egy oszlopot. Bármely sor vagy oszlop alapján meghatározható a determináns.
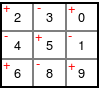
Legyen a példa kedvéért a következő mátrix:
A bal felső sarkot jelöljük meg „+” jellel. Ez után sakktábla-szerűen a többit is:
Vegyük a kifejtéshez az első oszlopot: 2, 4, 6.
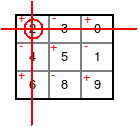
Jelöljük meg közülük az elsőt, azaz a 2-t. A 2-vel azonos sorban és oszlopban lévő elemekkel nem foglalkozunk. Így marad egy 2×2-es mátrix:
Ennek kiszámítjuk a determinánsát a 2×2 nagyságú mátrix esetén tanultak alapján.
Írjuk fel a fentebb kiválasztott 2-es számot és ezt a 37-es eredményt szorzatként:
2 * 37
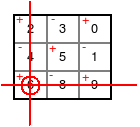
Vegyük az oszlop következő elemét, ami 4. A 4-gyel azonos sorokkal és oszlopokkal most nem foglalkozunk. A megmaradt elemek egy megint egy 2×2-es mátrixot alkotnak, aminek kiszámítjuk a determinánsát.
A 2 * 37 szorzathoz hozzáadjuk az újabbat:
A táblázatból látjuk, hogy a 4-es érték negatívan számít.
Vegyük az oszlop utolsó elemét, amely a 6. A hozzátartozó sor és oszlop elemeivel itt sem foglalkozunk:
Kiszámítjuk a megmaradt 2×2-es mátrix determinánsát:
A fenti szorzatunkhoz hozzáadjuk a 6 * 3 szorzatot. A 6 itt is az oszlop utolsó eleme, a 27 pedig az utóbbi 2×2-es mátrix determinánsa.
A szorzatunk végül:
Kiszámítva megkapjuk a determinánst:
A 3×3-as mátrixunk determináns számítás eredménye ezek után így írható fel:
4x4-s mátrix
A 4×4-s mátrixot úgy kezdjük mint a 3×3 méret esetén, de most négy oszloppal és sorral számolok. Az elsőként kiválasztott elem esetén, a kiválasztott elemhez tartozó sorok és oszlopokon kívül eső rész nem 2×2-s mátrix, helyette 3×3. A 3×3-as mátrix determinánsát a kifejtési tétellel számoljuk, mint azt az előbb láttuk.
Így járok el a többi sor és oszlop esetén is.
Java megvalósítás
//Determináns számítása: static double det(double[][] a, int n) { double d = 1; for(int k=0; k<n; k++){ for(int i=k+1; i<n; i++) { double g = a[i][k] / a[k][k]; for(int j=k+1; j<n; j++) { a[i][j] = a[i][j] - g * a[k][j]; } } d = d * a[k][k]; } return d; }
Mátrix típusok
Skalármátrix
1×1 dimenziós mátrix. Valójában egy szimpla szám.
Oszlopmátrix
Sormátrix
Négyzetes mátrix
Másként kvadratikus mátrix. A mátrix n x n elemből áll.
Nullmátrix
A nullmátrix minden eleme 0.
Egységmátrix
A főátlóban 1-es értékek vannak, a többi 0.
Felső háromszögmátrix
Az átló alatt 0 értékek.
Alsó háromszögmátrix
Az átló fölött nulla értékek.
Diagonális mátrix
A főátlón kívül minden elem 0;
Mátrix transzponáltja
Transzponálás
A transzponálás a sorok és oszlopok felcserélése.
| a mátrix (kiindulási táblázat) | |||
|---|---|---|---|
| 5 | 2 | 3 | 4 |
| 0 | 1 | 4 | 5 |
| 3 | 2 | 0 | 6 |
A transzponáltja:
| b mátrix (a transzponált) | ||
|---|---|---|
| 5 | 0 | 3 |
| 2 | 1 | 2 |
| 3 | 4 | 0 |
| 4 | 5 | 6 |
Java megvalósítás
- Program01.java
class Program01 { static int[][] a = { {5, 2, 3, 4}, {0, 1, 4, 5}, {3, 2, 0, 6}}; static int[][] b = new int[4][3]; public static void transzponal() { for(int i=0; i<3; i++) { for(int j=0; j<4; j++) { b[j][i] = a[i][j]; } } } public static void kiir(int sor, int oszlop, int[][] matrix) { for(int i=0; i<sor; i++) { for(int j=0; j<oszlop; j++) { System.out.print(matrix[i][j] + " "); } System.out.println(); } } public static void main(String[] args) { kiir(3, 4, a); System.out.println("------------"); transzponal(); kiir(4, 3, b); } }
Eredmény:
5 2 3 4 0 1 4 5 3 2 0 6 ------------ 5 0 3 2 1 2 3 4 0 4 5 6
Mátrix szorzata
Szorzás
Meg kell vizsgálnunk a szorzás elvégezhető-e.
A következő nagyságú mátrixok szorozhatók:
n * k és k * m
Ahol n*k az első mátrix méretei, és k*m a másik mátrix méretei. A két mátrix akkor szorozható, ha k méreteik megegyeznek. Az összeszorzott mátrix mérete: n * m lesz.
n * k és k * m eredmény: n * m
Mátrix műveletek
- Nem kommutatív a szorzásra nézve→ A * B != B * A
- Asszociatív → (A * B) * C = A * (B * C)
Mátrixok szorzása
Megvalósítás Java nyelven
- Program01.java
class Program01 { static int[][] a = { {1, 2}, {3, 4} }; static int[][] b = { {10, 20, 30}, {40, 50, 60} }; static int[][] c = new int[2][3]; public static void szoroz() { int m = 2, n = 2, k = 3; //m-oszlop, n-sor (k-oszlop) int sum=0; for (int i = 0 ; i < n ; i++ ) { for (int j = 0 ; j < k ; j++ ) { for (int p = 0 ; p < m ; p++ ) { sum = sum + a[i][p] * b[p][j]; } c[i][j] = sum; sum = 0; } } } public static void kiir(int sor, int oszlop, int[][] matrix) { for(int i=0; i<sor; i++) { for(int j=0; j<oszlop; j++) { System.out.print(matrix[i][j] + " "); } System.out.println(); } } public static void main(String[] args) { kiir(2, 2, a); System.out.println("------------"); kiir(2, 3, b); System.out.println("------------"); szoroz(); kiir(2, 3, c); } }
Eredmény:
1 2 3 4 ------------ 10 20 30 40 50 60 ------------ 90 120 150 190 260 330
Mátrix inverze
Az invertálásról
Keressük azt a mátrixot, amelyet megszorozva az eredeti mátrixot, az egységmátrixot kapjuk.
Az eredmények közönséges törtként:
Az eredmények tizedestörtként:
Invertálás Gauss–Jordan-eliminációval
Legyen A mátrix. Keressük az inverzét, amit így jelölünk: A-1
Egy mátrix nem invertálható ha a determinánsa 0.
Ezért számítsuk ki a determinánst:
det A = 2 * 4 - 3 * 1 = 5 ≠ 0
Nem nulla, így a mátrix invertálható.
Leírjuk az A mátrixot és mellé az E egységmátrixot:
[A|E]
Osztjuk az első sort 2-vel:
Hozzáadjuk a második sorhoz az első -3 szorosát:
Osztjuk a második sort 5/2-vel:
Hozzáadjuk az első sorhoz, második sor -1/2 szeresét:
Az eredmény:
A-1 =
Java Megvalósítás
- Program01.java
import java.util.Scanner; class Program01 { public static void main(String[] args) { Scanner in = new Scanner(System.in); System.out.println("Mátrix invertálása"); System.out.print("Mátrix mérete: "); int size = in.nextInt(); double[][] a = new double[size][size+size]; //Az egységmátrix elkészítése for (int i = 0; i < size; i++) { for (int j = 0; j < size+size; j++) { if (j == i + size) { a[i][j] = 1; } else { a[i][j] = 0; } } } //Mátrix bekérése System.out.printf("\nÍrd be a %d X %d mátrixot:\n", size, size); for (int i = 0; i < size; i++) { for (int j = 0; j < size; j++) { a[i][j] = in.nextDouble(); } } if(det(a, size)==0) { System.out.println("Nem invertálható, mert a determinánsa 0"); }else { inverz(a, size); kiir(a, size); } } //Determináns számítása: static double det(double[][] a, int n) { double d = 1; for(int k=0; k<n; k++){ for(int i=k+1; i<n; i++) { double g = a[i][k] / a[k][k]; for(int j=k+1; j<n; j++) { a[i][j] = a[i][j] - g * a[k][j]; } } d = d * a[k][k]; } return d; } static void inverz(double[][] a, int size) { //Oszloponként változtatok for (int i = 0; i < size; i++) { reduction(a, size, i, i); } } static void kiir(double[][] a, int size) { System.out.println("\nInverz mátrix"); for (int i = 0; i < size; i++) { for (int j = 0; j < size; j++) { System.out.printf("%8.2f", a[i][j + size]); } System.out.println(); } } static void reduction(double a[][], int size, int pivot, int col) { double factor = a[pivot][col]; for (int i = 0; i < 2 * size; i++) { a[pivot][i] /= factor; } for (int i = 0; i < size; i++) { if (i != pivot) { factor = a[i][col]; for (int j = 0; j < 2 * size; j++) { a[i][j] = a[i][j] - a[pivot][j] * factor; } } } } }
Függelék
Mátrix invertálás példa
| mátrix | ||
|---|---|---|
| 7 | 1 | 1 |
| 1 | 3 | 2 |
| 6 | 4 | 1 |
Gauss-Jordan elimináció
| Hozzáadjuk az egységmátrixot | |||||
|---|---|---|---|---|---|
| 7 | 1 | 1 | 1 | 0 | 0 |
| 1 | 3 | 2 | 0 | 1 | 0 |
| 6 | 4 | 1 | 0 | 0 | 1 |
Az első sort osztom 7-tel:
| 1sor = 1sor/7 | |||||
|---|---|---|---|---|---|
| 1 | 1/7 | 1/7 | 1/7 | 0 | 0 |
| 1 | 3 | 2 | 0 | 1 | 0 |
| 6 | 4 | 1 | 0 | 0 | 1 |
Hozzáadjuk a kettes sorhoz az első sor -1 szeresét:
| 2sor = 1sor * -1 + 2sor | |||||
|---|---|---|---|---|---|
| 1 | 1/7 | 1/7 | 1/7 | 0 | 0 |
| 0 | 20/7 | 13/7 | -1/7 | 1 | 0 |
| 6 | 4 | 1 | 0 | 0 | 1 |
| 3sor = 1sor * -6 + 3sor | |||||
|---|---|---|---|---|---|
| 1 | 1/7 | 1/7 | 1/7 | 0 | 0 |
| 0 | 20/7 | 13/7 | -1/7 | 1 | 0 |
| 0 | 22/7 | 1/7 | -6/7 | 0 | 1 |
| 2sor = 2sor : 20/7 | |||||
|---|---|---|---|---|---|
| 1 | 1/7 | 1/7 | 1/7 | 0 | 0 |
| 0 | 1 | 13/20 | -1/20 | 7/20 | 0 |
| 0 | 22/7 | 1/7 | -6/7 | 0 | 1 |
| 3sor = 2sor * -22/7 + 3sor | |||||
|---|---|---|---|---|---|
| 1 | 1/7 | 1/7 | 1/7 | 0 | 0 |
| 0 | 1 | 13/20 | -1/20 | 7/20 | 0 |
| 0 | 0 | -19/10 | -7/10 | -11/10 | 1 |
| 3sor = 3sor : -19/10 | |||||
|---|---|---|---|---|---|
| 1 | 1/7 | 1/7 | 1/7 | 0 | 0 |
| 0 | 1 | 13/20 | -1/20 | 7/20 | 0 |
| 0 | 0 | 1 | 7/19 | 11/19 | -10/19 |
| 2sor = 3sor * -13/20 + 2sor | |||||
|---|---|---|---|---|---|
| 1 | 1/7 | 1/7 | 1/7 | 0 | 0 |
| 0 | 1 | 0 | -11/38 | -1/38 | 13/38 |
| 0 | 0 | 1 | 7/19 | 11/19 | -10/19 |
| 1sor = 3sor * -1/7 + 1sor | |||||
|---|---|---|---|---|---|
| 1 | 1/7 | 0 | 12/133 | -11/133 | 10/133 |
| 0 | 1 | 0 | -11/38 | -1/38 | 13/38 |
| 0 | 0 | 1 | 7/19 | 11/19 | -10/19 |
| 1sor = 2sor * -1/7 + 1sor | |||||
|---|---|---|---|---|---|
| 1 | 0 | 0 | 5/38 | -3/38 | 1/38 |
| 0 | 1 | 0 | -11/38 | -1/38 | 13/38 |
| 0 | 0 | 1 | 7/19 | 11/19 | -10/19 |
A mátrix inverze:
| Eredmény | ||
|---|---|---|
| 5/38 | -3/38 | 1/38 |
| -11/38 | -1/38 | 13/38 |
| 7/19 | 11/19 | -10/19 |
Mátrix invertálás példa 2
| mátrix | |
|---|---|
| 1 | 2 |
| 3 | 4 |
Gauss-Jordan elimináció
| Hozzáadjuk az egységmátrixot | |||
|---|---|---|---|
| 1 | 2 | 1 | 0 |
| 3 | 4 | 0 | 1 |
| 2sor = (1sor * -3) + 2sor | |||
|---|---|---|---|
| 1 | 2 | 1 | 0 |
| 0 | -2 | -3 | 1 |
A második sort osztom -2-vel:
| 2sor = 2sor : -2 | |||
|---|---|---|---|
| 1 | 2 | 1 | 0 |
| 0 | 1 | 3/2 | -1/2 |
| 1sor = (2sor * -2) + 1 | |||
|---|---|---|---|
| 1 | 0 | -2 | 1 |
| 0 | 1 | 3/2 | -1/2 |
| Eredmény | |
|---|---|
| -2 | 1 |
| 3/2 | -1/2 |
Mátrix invertálás példa 3
| mátrix | |
|---|---|
| 5 | 2 |
| 3 | 6 |
Gauss-Jordan elimináció
| Hozzáadjuk az egységmátrixot | |||
|---|---|---|---|
| 5 | 2 | 1 | 0 |
| 3 | 6 | 0 | 1 |
| 1sor = 1sor : 5 | |||
|---|---|---|---|
| 1 | 2/5 | 1/5 | 0 |
| 3 | 6 | 0 | 1 |
| 2sor = (1sor * -3) + 2sor | |||
|---|---|---|---|
| 1 | 2/5 | 1/5 | 0 |
| 0 | 24/5 | -3/5 | 1 |
| 2sor = 2sor : 24/5 | |||
|---|---|---|---|
| 1 | 2/5 | 1/5 | 0 |
| 0 | 1 | -1/8 | 5/24 |
| 1sor = (2sor * -2/5) + 1sor | |||
|---|---|---|---|
| 1 | 0 | 1/4 | -1/12 |
| 0 | 1 | -1/8 | 5/24 |
| Eredmény | |
|---|---|
| 1/4 | -1/12 |
| -1/8 | 5/24 |