Tartalomjegyzék
Lengyelforma
- Szerző: Sallai András
- Copyright © 2014, Sallai András
- Licenc: CC BY-SA 4.0
- Web: https://szit.hu
A lengyelformáról
A lengyelforma, angolul polish notation, Jan Łukasiweicz matematikus munkája, amit az 1920-as években kutatott. A lengyelforma az aritmetikai kifejezések felírása olyan formában, hogy az operátorok az operandusokat megelőzi.
A 3 + 2 helyett a következőt írom: + 3 2. Az informatikában a fordított lengyelformát használjuk, vagyis az operátorokat az operandusok után írjuk: 3 2 +. A fordított lengyelforma angolul Reverse Polish Notation, röviden RPN, amit angol nyelv területen gyakran használnak. A magyar nyelvben általában csak lengyelformaként említik.
Az aritmetikai kifejezések hagyományos írásának az elnevezése infix forma. Ha az operátorokat az operandusok elé írjuk, akkor prefix formáról beszélünk. Ha az operátorokat az operandusok után írjuk, akkor postfix formáról beszélünk.
| Infix jelölés |
|---|
| 3 + 2 |
| Prefix jelölés |
|---|
| + 3 2 |
| Postfix jelölés |
|---|
| 3 2 + |
A lengyelforma és a zárójelek
A lengyelformában nem használunk zárójeleket. A sorrend meghatározza a műveletek sorrendjét. Ránézésre ez kissé átláthatatlanabb, de a számítógép számára könnyebben feldolgozható, és kevés művelet esetén jobb feldolgozási időt produkál.
A következő példákban a zárójelek eltűnését láthatjuk a postfix formában:
- infix: 2 * ( 2 + 1 ) ^ 2
- postfix: 2 2 1 + 2 ^ *
Az algoritmusról
A lengyelformára konvertáló legnevesebb algoritmus angolul Shunting-yard, ami pályaudvarnak fordítható. Lengyelforma kiértékelő algoritmust evalRPN néven találjuk meg. Mindkét algoritmust veremmel valósítjuk meg.
A következő képen a Shuting-yard algoritmust látjuk működés közben:
Java megvalósítás
Lengyelformára konvertálás
static String infixToPostfix(String infix) { final String operators = "-+/*^"; StringBuilder output = new StringBuilder(); Stack<String> verem = new Stack<String>(); StringTokenizer infixTokens = new StringTokenizer(infix, " "); while (infixTokens.hasMoreTokens()) { String token = infixTokens.nextToken(); //Ha operátor if(operators.contains(token)) { //Ha üres a verem, akkor az operátor megy a verembe if (verem.isEmpty()) { verem.push(token); }else { // Ha nem üres, megnézzük mi a prioritása // a verem tetején lévőhöz képest while (!verem.isEmpty()) { int priorityTopStack = operators.indexOf(verem.peek()); int priorityToken = operators.indexOf(token); // Ha verem tetején az operátornak nagyobb prioritása, // akkor előbb azt fűzzük a kimenethez if (priorityTopStack >= priorityToken){ output.append(verem.pop()); output.append(' '); } else break; } verem.push(token); } } else if(token.equals("(")) { //Szimpla nyitó zárójelet a verembe tesszük verem.push(token); } else if(token.equals(")")) { // Ha bezáró zárójelet találunk, akkor a vermet // a kimenetre ürítjük egy nyitózárójelig while (!verem.peek().equals("(")) { output.append(verem.pop() + " "); } verem.pop(); //zárójelet eldobjuk } else { output.append(token + " "); } } // Végül kiürítjük a vermet, // ha még van benne valami, a kimenetre while (!verem.isEmpty()) { output.append(verem.pop() + " "); } return output.toString(); }
Érték számítása
static double evalPostfix(String postfix) { final String operators = "-+/*^"; Double result = 0.0; Stack<String> stack = new Stack<String>(); StringTokenizer postfixTokens = new StringTokenizer(postfix, " "); while(postfixTokens.hasMoreTokens()) { String token = postfixTokens.nextToken(); if(operators.contains(token)) { double num2 = Double.parseDouble(stack.pop()); double num1 = Double.parseDouble(stack.pop()); switch (token) { case "+" : result = num1 + num2; break; case "-" : result = num1 - num2; break; case "/" : result = num1 / num2; break; case "*" : result = num1 * num2; break; case "^" : result = Math.pow(num1, num2); break; } stack.push(result.toString()); }else { stack.push(token); } } return result; }
Kifejezés tárolása bináris fában
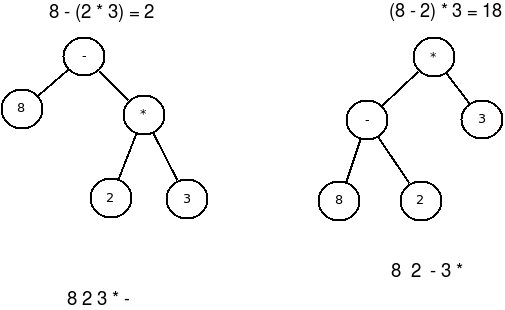
A lengyelformát tárolhatjuk fában
A levelek szintjén találjuk a operandusokat, a csúcsokban pedig a műveleteket. A fában nem tárolunk zárójeleket, mégis egyértelmű lehet, melyik műveletet kell elsőként elvégezni.
A következő táblázatokban a előbbi ábra két fájának bejárásával kapott kifejezéseket láthatjuk:
| preorder bejárás | |
|---|---|
| bal oldali | jobb oldali |
| - 8 * 2 3 | * - 8 2 3 |
| |
|
|---|---|
| bal oldali | jobb oldali |
| 8 - 2 * 3 | 8 - 2 * 3 |
| postorder bejárás | |
|---|---|
| bal oldali | jobb oldali |
| 8 2 3 * - | 8 2 - 3 * |
Az eredményekből látható, hogy az inorder bejárás alkalmatlan a kifejezés egyértelmű visszafejtésére.